Baumdiagramme mit Textverarbeitung

Graphische Darstellung von Baumdiagrammen

Der Ablauf eines mehrstufigen Zufallsversuchs lässt sich mithilfe von sogenannten Baumdiagrammen besonders übersichtlich darstellen. Dies wird im Folgenden am Beispiel eines zweistufigen Experiments erläutert, nämlich dem zweimaligen Werfen eines Würfels. Dabei werden bei jedem Wurf nur zwei Ergebnisse betrachtet, nämlich:

H ="Zahl ist hoch" ="Zahl ist 5 oder 6" und

T = "Zahl ist tief" ="Zahl liegt zwischen 1 und 4 einschließlich"

Es ist also \Omega = \{HH, HT, TH, TT \}

Betrachtet man die Wahrscheinlichkeiten innerhalb einer einzigen Stufe, so erkennt man leicht:

Die Wahrscheinlichkeit für das Ergebnis T in einem Wurf beträgt P(T) =2/3 und die Wahrscheinlichkeit für das Ergebnis H ist P(H) =1/3.

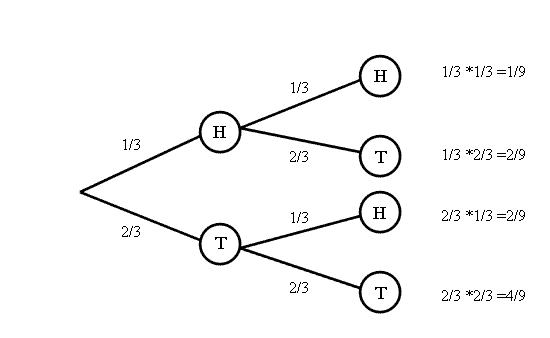
Der zugehörige Ereignisbaum sieht dann so aus:

Beschreibung des Baumdiagramms in Worten

Das Bild zeigt den entsprechenden Ereignisbaum, der von links nach rechts "wächst". Ausgehend von der gemeinsamen Wurzel (links) führen zunächst zwei Linien (Zweige) zu den beiden Ergebnissen den 1. Stufe, nämlich zum Ergebnis H (nach rechts oben) und T (nach rechts unten). Jeder Zweig ist mit der entsprechenden Wahrscheinlichkeit beschriftet, also der Zweig nach H mit dem Wert 1/3 und der Zweig nach T mit dem Wert 2/3.

Von H aus führen nun zwei weitere Zweige zu den Ergebnissen der 2. Stufe, also wieder nach rechts oben zum Ergebnis H und nach rechts unten zum Ergebnis T. Auch hier sind die Zweige wieder mit den entsprechenden Wahrscheinlichkeiten 1/3 bzw. 2/3 beschriftet. Ganz analog führen auch vom Ergebnis T der 1. Stufe zwei beschriftete Zweige weiter nach rechts zu den Ergebnissen H und T der 2. Stufe.

Baumdiagramme in der Informatik

Auch in der Informatik werden häufig hierarchische Bäume zur Veranschaulichung von Sachverhalten verwendet. Dabei werden die Punkte, die durch die Zweige verbunden werden, als "Knoten" bezeichnet. Der Ausgangspunkt ganz links heißt "Wurzel", die Endpunkte ganz rechts heißen "Blätter". Eine Kette von Zweigen, die von der Wurzel bis zu einem Blatt reicht, wird als Pfad bezeichnet.

Bei einem n-stufigen Versuch besteht jeder Pfad aus genau n Zweigen, d.h. jeder Pfad entspricht einem Ergebnis des mehrstufigen Versuchs.

Darstellung in Textform

Der oben beschriebene Baum kann folgendermaßen leicht in Textform dargestellt werden:

HH 1/3 *1/3

HT 1/3 *2/3

TH 2/3 *1/3

TT 2/3 *2/3

Jeder Zweig wird dabei in einer eigenen Zeile dargestellt.

Die Ergebnisse innerhalb eines Zweiges werden in der Reihenfolge der Stufen aufgelistet. Die Wahrscheinlichkeiten der Ergebnisse pro Stufe werden hinter der Ereignis-Liste in entsprechender Reihenfolge aufgelistet und durch das Multiplikationszeichen * verbunden.

Beispielaufgabe Multiple-Choice-Test

Bei einem Multiple-Choice-Test werden zu jeder der drei Fragen drei Antwortmöglichkeiten angeboten, von denen stets genau eine richtig ist. Der Test gilt als bestanden, wenn mindestens zwei der drei Fragen richtig beantwortet werden. Mit welcher Wahrscheinlichkeit besteht man den Test bei zufälligem Ankreuzen?

Hier die drei Testfragen:

1. Wie viel Joule (J) sind 1 Kalorie?

4,176 J [ ]    4,168 J [ ]   4,187 J [ ]

2. Wann wurde der Physiker Bragg geboren?

1842 [ ]   1862 [ ]    1852 [ ]

3. Wie groß ist die Schallgeschwindigkeit in Gold?

2030 m/s [ ]    5080 m/s [ ]   1200 m/s [ ]

Lösung Multiple-Choice-Test

Wir stellen den Ablauf des dreistufigen Zufallsexperimentes in einem Wahrscheinlichkeitsbaum dar. Dabei sei R ="richtige Antwort" und F =" falsche Antwort". In jeder Stufe (bei jeder Frage) gilt: P(R) =1/3, P(F) =2/3. Die zu E gehörenden Ergebnisse werden wieder mit dem Zusatz "\in E" gekennzeichnet:

Baumdiagramm:

RRR 1/3 *1/3 *1/3 =1/27 \in E

RRF 1/3 *1/3 *2/3 =2/27 \in E

RFR 1/3 *2/3 *1/3 =2/27 \in E

RFF 1/3 *2/3 *2/3 =4/27

FRR 2/3 *1/3 *1/3 =2/27 \in E

FRF 2/3 *1/3 *2/3 =4/27

FFR 2/3 *2/3 *1/3 =4/27

FFF 2/3 *2/3 *2/3 =8/27

Als Wahrscheinlichkeit von E erhält man mit der Pfadregel:

P("mind. 2R") =1/27 +2/27 +2/27 +2/27 =7/27

Das Ereignis E: "Der Test wird bestanden" hat die Wahrscheinlichkeit P(E) =7/27. Man hat also eine Chance von ca. 26 %, den Test auch ohne entsprechende Kenntnisse bestehen zu können.

Baumdiagramm schrittweise in Textform erstellen

Bei der Bearbeitung von Wahrscheinlichkeitsaufgaben ist es häufig sinnvoll, zunächst ein Baumdiagramm zu erstellen. Im Folgenden wird am Beispiel Multiple-Choice-Test erläutert, wie man ein Baumdiagramm in Textform schrittweise selbst entwickeln kann.

1. Schritt

Man identifiziert alle Ergebnisse innerhalb einer Stufe und schreibt diese zeilenweise untereinander. Im Beispiel erhält man einen Block aus zwei Zeilen:

--- schnipp ---

R

F

--- schnapp ---

2. Schritt

Man vervielfacht diesen Block aus zwei Zeilen so, dass man so viele Blöcke erhält wie es Ergebnisse pro Stufe gibt. Im Beispiel gibt es zwei Ergebnisse pro Stufe, also wird der zweizeilige Block einfach verdoppelt. In einem Textverarbeitungsprogramm lässt sich dies leicht durch Markieren der Zeilen, Kopieren und Einfügen erreichen:

--- schnipp ---

R

F

R

F

--- schnapp ---

3. Schritt

Man stellt nun jeder Zeile des ersten Blocks das erste Stufenergebnis voran, jeder Zeile des zweiten Blocks das zweite Stufenergebnis usw. so dass sich anschließend wieder alle Zeilen unterscheiden:

--- schnipp ---

RR

RF

FR

FF

--- schnapp ---

4. Schritt

Bei jeder weiteren Stufe verfährt man nun zunächst wieder wie im 2. Schritt, d.h. man betrachtet alle bisher vorhanden Zeilen als einen Block und vervielfacht diesen entsprechend der Anzahl der Ergebnisse pro Stufe:

--- schnipp ---

RR

RF

FR

FF

RR

RF

FR

FF

--- schnapp ---

Nun stellt man analog zum 3. Schritt blockweise die Stufenergebnisse vor jede Zeile, so dass anschließend alle Zeilen wieder verschieden sind:

--- schnipp ---

RRR

RRF

RFR

RFF

FRR

FRF

FFR

FFF

--- schnapp ---

Diesen Vorgang wiederholt man mit jeder weiteren Stufe.

Anmerkung: Auf einer Bogenmaschine ist es schwierig, Zeichen am Zeilenanfang einzufügen. Man müsste hier von vornherein am Zeilenanfang eine genügend große Lücke lassen, die dann schrittweise von rechts nach links aufgefüllt wird. Schreibtechnisch etwas einfacher ist es, wenn man stattdessen die Zeichen schrittweise jeweils am Zeilenende anfügt. Auf diese Weise entsteht allerdings ein gespiegelter Baum, der quasi von rechts nach links wächst.

5. Schritt

Die Wahrscheinlichkeiten der Ergebnisse pro Stufe werden zeilenweise hinzugefügt. Dabei ist zu beachten, ob die Wahrscheinlichkeiten von Stufe zu Stufe gleich bleiben (z.B. beim Ziehen mit Zurücklegen) oder ob sie sich ändern (z.B. beim Ziehen ohne Zurücklegen).

--- schnipp ---

RRR 1/3 *1/3 *1/3

RRF 1/3 *1/3 *2/3

RFR 1/3 *2/3 *1/3

RFF 1/3 *2/3 *2/3

FRR 2/3 *1/3 *1/3

FRF 2/3 *1/3 *2/3

FFR 2/3 *2/3 *1/3

FFF 2/3 *2/3 *2/3

--- schnapp ---

6. Schritt

Schließlich werden die Pfadwahrscheinlichkeiten ausgerechnet, die zum betrachteten Ereignis E gehörenden Ergebnisse werden markiert und deren Pfadwahrscheinlichkeiten addiert:

--- schnipp ---

RRR 1/3 *1/3 *1/3 =1/27 \in E

RRF 1/3 *1/3 *2/3 =2/27 \in E

RFR 1/3 *2/3 *1/3 =2/27 \in E

RFF 1/3 *2/3 *2/3 =4/27

FRR 2/3 *1/3 *1/3 =2/27 \in E

FRF 2/3 *1/3 *2/3 =4/27

FFR 2/3 *2/3 *1/3 =4/27

FFF 2/3 *2/3 *2/3 =8/27

--- schnapp ---

P(E) =P("mind. 2R") =1/27 +2/27 +2/27 +2/27 =7/27

Zur Kontrolle kann man im vollständigen Baumdiagramm alle Pfadwahrscheinlichkeiten addieren. Die Summe muss 1 ergeben:

1/27 +2/27 +2/27 +4/27 +2/27 +4/27 +4/27 +8/27 =27/27 =1